mc110-1.jpg To the nearest tenth, what is the area of the shaded segment when AG = 6 ft?
Area & Perimeter of a Rectangle computer uses length and width of a rectangle, and calculates the perimeter, area and diagonal length of the rectangle. Information technology is an online Geometry tool requires two length sides of a rectangle. Using this figurer, we will sympathise the algorithm of how to find the perimeter, area and diagonal length of a rectangle.
Information technology is necessary to follow the next steps:
- Enter the length and width of a rectangle in the box. These values must exist positive existent numbers or parameter. Notation that the length of a segment is e'er positive;
- Press the "GENERATE WORK" button to make the computation;
- Rectangle reckoner volition requite the perimeter, expanse and diagonal length of a rectangle.
Input : Ii positive existent numbers or parameters as the length and width of a rectangle;
Output : Three positive real numbers or variables equally the perimeter, area and diagonal length of a rectangle and corresponding units after that.
Rectangle Formula :
Perimeter of Rectangle Formula: The perimeter of a rectangle is determined by the following formula
$$P=2\times a+2\times b=2\times(a+b)$$
where $a$ and $b$ are the length and width of the rectangle, respectively.
Area of Rectangle Formula: The expanse of a rectangle is determined past the following formula
$$A=a\times b$$
where $a$ and $b$ are the length and width of the rectangle, respectively.
Length of Diagonal of Rectangle Formula: The diagonal of a rectangle is determined by the post-obit formula
$$d=\sqrt{a^2+b^two}$$
where $a$ and $b$ are the length and width of the rectangle, respectively.
What is Area & Perimeter of Rectangle?
A quadrilateral with 4 coinciding angles is a rectangle. The give-and-take "rectangle" comes from Latin "rectangulus". Information technology'southward a combination of "rectus" which means "right" and "angulus" which means "an angle".
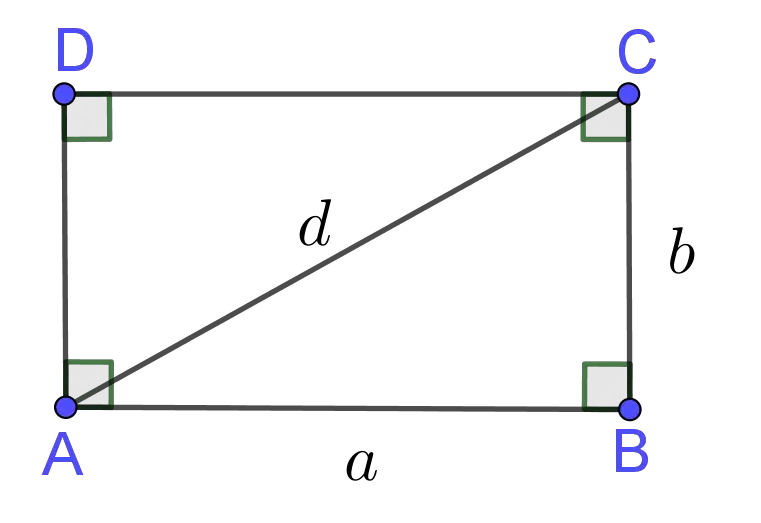
If $\angle A\cong\angle B\cong\bending C\cong\angle D$, then ${\overline{ABCD}}$ is a rectangle (see the picture below). It holds that
$$k\angle A=thou\angle B=m\angle C=m\angle D=\frac{{360}^o}{4}={90}^o$$

The lengths of its sides are denoted by $a$ and $b$, while the length of the diagonal is denoted with $d$. A rectangle is besides called an equiangular quadrilateral, since all of its angles are congruent.
A rectangle is a parallelogram, merely parallelogram is not a rectangle considering in a rectangle each angle is a right bending, whereas it is not so in a parallelogram. That ways that all the backdrop of a parallelogram can exist as well applied to rectangles. To recall, the parallelogram has the following properties:
- Reverse sides of a parallelogram are congruent;
- Contrary angles of a parallelogram are congruent;
- The consecutive angles of a parallelogram are supplementary to each other;
- The diagonals of a parallelogram bisect each other
Rectangle satisfies one more belongings:
- The diagonals of a rectangle are congruent;
If we know side lengths of the rectangle, it is easy to summate the length of the diagonal using the Pythagorean Theorem. A diagonal divides a rectangle into ii right triangles. By applying the Pythagorean Theorem to $\Delta ABC$, nosotros get
$$d^2={\overline{AB}}^ii+{\overline{BC}}^2=a^2+b^ii$$
i.e.
$$d=\sqrt{a^2+b^2}$$
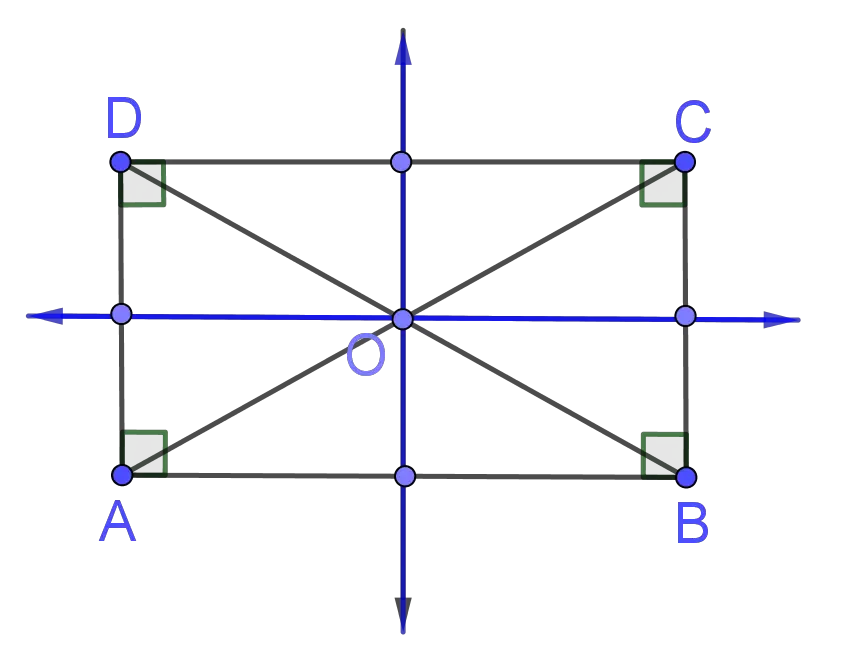
The rectangle has only two lines of symmetry. These lines are these ones which connect the midpoints of the opposite sides of the rectangle. A rectangle has central symmetry and rotational symmetry. The center of symmetry is the point of intersection of its diagonals, $O$.
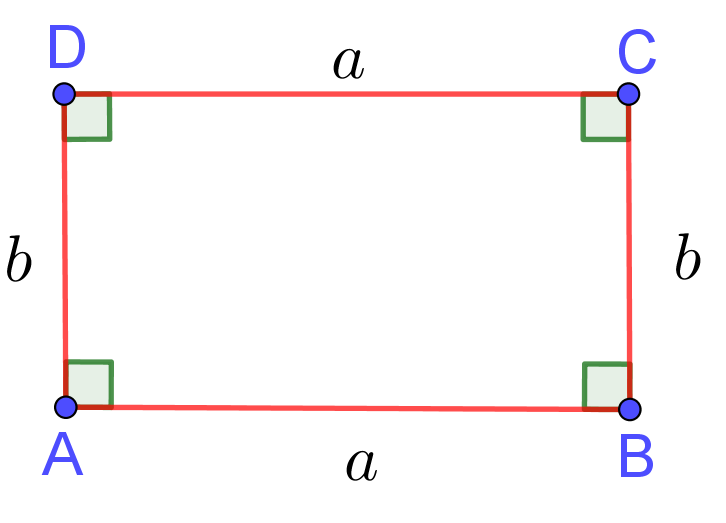
The distance around a rectangle is called the perimeter of the rectangle. It is usually denoted by $P$. To detect the perimeter of rectangle we add the lengths of its sides. Thus, the perimeter of a rectangle with the length of $a$ and the width of $b$ is
$$P =a+b+a+b= 2 \times a+2\times b=2\times(a+b)$$
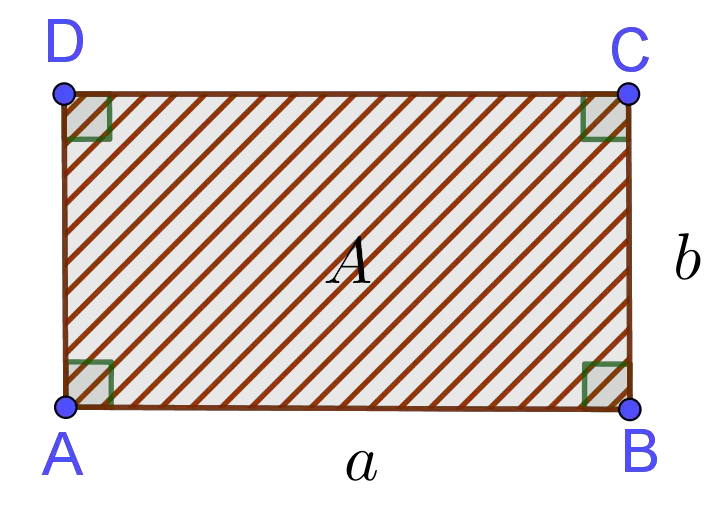
The area of a rectangle or some other polygon is a number of foursquare units needed to fill the rectangle. The area, unremarkably denoted by $A$, of a rectangle with the length of $a$ and the width of $b$ is
$$A =\mbox{length}\times\mbox{width}=a\times b$$
In other words, the expanse of a rectangle is the production of its length and width.
The perimeter is measured in units such as centimeters, meters, kilometers, inches, anxiety, yards, and miles. The area is measured in units units such as square centimeters $(cm^2)$, square meters $(one thousand^2)$, square kilometers $(km^2)$ etc.
The area and perimeter of a rectangle work with steps shows the complete step-by-stride calculation for finding the perimeter, area and diagonal length of the rectangle with the length of $v\;in$ and the width of $10 \;in$ using the perimeter, area and diagonal length formulas. For any other values for length and width of rectangle, just supply 2 positive real numbers and click on the GENERATE WORK push. The course school students may use this area and perimeter of a rectangle to generate the work, verify the results of perimeter and area of two dimensional figures or do their homework problems efficiently.
Real World Issues Using Area & Perimeter of a Rectangle
Calculating areas and perimeters of various geometrical figures are very useful in real life problems. Rectangles often appear in real life. For instance, billboards, pond pools, mobile phones, beds, doors, books. etc. If nosotros need to make a deck forth two sides of a swimming pool of rectangular shape, we must use the method for finding surface area of rectangle.
In three-dimensional geometry, some solids contains rectangular bases. For example, cube, rectangular prism, pyramid, etc. In problems of calculating surface expanse and volume of these solids we use formula for finding area of rectangle.
Rectangle Practice Issues
Practice Trouble 1:
A rectangular garden is $2$ times long as its wide. If the perimeter of the garden is $48m$, find its surface area.
Practice Problem ii:
Discover the length of the diagonal of a floor whose dimensions are $36\;in$ past $75\;in$.
The Area Perimeter of a Rectangle estimator, formula, case calculation (work with steps), real world problems and do problems would be very useful for class school students (K-12 education) to understand the concept of perimeter and area of rectangle. This concept can exist of significance in geometry, to find the perimeter and area of complex figures, likewise every bit to find area and book of some solids. Real life problems on rectangles involving length, width, area, perimeter and diagonal are very common, so this can be of great the importance of solving.
Source: https://ncalculators.com/geometry/rectangle-calculator.htm
0 Response to "mc110-1.jpg To the nearest tenth, what is the area of the shaded segment when AG = 6 ft?"
Post a Comment